아이템 줍기

코딩 테스트/Level 3 2021. 10. 20. 07:50

https://programmers.co.kr/learn/courses/30/lessons/87694

코딩테스트 연습 - 11주차

[[1,1,7,4],[3,2,5,5],[4,3,6,9],[2,6,8,8]] 1 3 7 8 17 [[1,1,8,4],[2,2,4,9],[3,6,9,8],[6,3,7,7]] 9 7 6 1 11 [[2,2,5,5],[1,3,6,4],[3,1,4,6]] 1 4 6 3 10

programmers.co.kr

파이썬

def solution(rectangle, char_x, char_y, item_x, item_y):
    limit_x, limit_y = 100, 100
    rectangles = tuple(make_double(r) for r in rectangle)
    char_x, char_y, item_x, item_y = make_double((char_x, char_y, item_x, item_y))
    moves = ((0, 1), (0, -1), (1, 0), (-1, 0))
    arrived = [[-2 for _ in range(limit_y + 1)] for _ in range(limit_x + 1)]
    for x1, y1, x2, y2 in rectangles:
        for rect_x in range(x1, x2 + 1):
            arrived[rect_x][y1] = arrived[rect_x][y2] = -1
        for rect_y in range(y1, y2 + 1):
            arrived[x1][rect_y] = arrived[x2][rect_y] = -1
    for x1, y1, x2, y2 in rectangles:
        for rect_x in range(x1 + 1, x2):
            for rect_y in range(y1 + 1, y2):
                arrived[rect_x][rect_y] = -2
    que = [(char_x, char_y, 0)]
    while que:
        (now_x, now_y, now_length) = que.pop(0)
        if arrived[now_x][now_y] != -1:
            continue
        arrived[now_x][now_y] = now_length
        if (now_x, now_y) == (item_x, item_y):
            break
        for move_x, move_y in moves:
            if 1 <= (next_x := now_x + move_x) <= limit_x and 1 <= (next_y := now_y + move_y) <= limit_y:
                que.append((next_x, next_y, now_length + 1))
    return arrived[item_x][item_y] // 2


def make_double(nums):
    return tuple(num * 2 for num in nums)

deque를 쓰는 것이 더 좋겠으나,
간략하게 코딩하기 위해 list를 사용했습니다.

테스트 1 〉	통과 (0.29ms, 10.3MB)
테스트 2 〉	통과 (0.33ms, 10.4MB)
테스트 3 〉	통과 (0.29ms, 10.3MB)
테스트 4 〉	통과 (0.29ms, 10.4MB)
테스트 5 〉	통과 (0.28ms, 10.3MB)
테스트 6 〉	통과 (0.29ms, 10.5MB)
테스트 7 〉	통과 (0.36ms, 10.4MB)
테스트 8 〉	통과 (0.37ms, 10.3MB)
테스트 9 〉	통과 (0.81ms, 10.4MB)
테스트 10 〉	통과 (0.82ms, 10.4MB)
테스트 11 〉	통과 (0.85ms, 10.4MB)
테스트 12 〉	통과 (0.86ms, 10.4MB)
테스트 13 〉	통과 (0.86ms, 10.4MB)
테스트 14 〉	통과 (0.49ms, 10.4MB)
테스트 15 〉	통과 (0.35ms, 10.4MB)
테스트 16 〉	통과 (0.68ms, 10.4MB)
테스트 17 〉	통과 (0.71ms, 10.4MB)
테스트 18 〉	통과 (0.79ms, 10.4MB)
테스트 19 〉	통과 (0.98ms, 10.4MB)
테스트 20 〉	통과 (1.02ms, 10.4MB)
테스트 21 〉	통과 (0.70ms, 10.4MB)
테스트 22 〉	통과 (0.55ms, 10.4MB)
테스트 23 〉	통과 (0.75ms, 10.4MB)
테스트 24 〉	통과 (0.76ms, 10.4MB)
테스트 25 〉	통과 (0.41ms, 10.5MB)
테스트 26 〉	통과 (0.40ms, 10.4MB)
테스트 27 〉	통과 (0.46ms, 10.4MB)
테스트 28 〉	통과 (0.45ms, 10.4MB)
테스트 29 〉	통과 (0.48ms, 10.3MB)
테스트 30 〉	통과 (0.42ms, 10.3MB)

deque를 사용하면..

from collections import deque


def solution(rectangle, char_x, char_y, item_x, item_y):
    limit_x, limit_y = 100, 100
    rectangles = tuple(make_double(r) for r in rectangle)
    char_x, char_y, item_x, item_y = make_double((char_x, char_y, item_x, item_y))
    moves = ((0, 1), (0, -1), (1, 0), (-1, 0))
    arrived = [[-2 for _ in range(limit_y + 1)] for _ in range(limit_x + 1)]
    for x1, y1, x2, y2 in rectangles:
        for rect_x in range(x1, x2 + 1):
            arrived[rect_x][y1] = arrived[rect_x][y2] = -1
        for rect_y in range(y1, y2 + 1):
            arrived[x1][rect_y] = arrived[x2][rect_y] = -1
    for x1, y1, x2, y2 in rectangles:
        for rect_x in range(x1 + 1, x2):
            for rect_y in range(y1 + 1, y2):
                arrived[rect_x][rect_y] = -2
    que = deque([(char_x, char_y, 0)])
    while que:
        (now_x, now_y, now_length) = que.popleft()
        if arrived[now_x][now_y] != -1:
            continue
        arrived[now_x][now_y] = now_length
        if (now_x, now_y) == (item_x, item_y):
            break
        for move_x, move_y in moves:
            if 1 <= (next_x := now_x + move_x) <= limit_x and 1 <= (next_y := now_y + move_y) <= limit_y:
                que.append((next_x, next_y, now_length + 1))
    return arrived[item_x][item_y] // 2


def make_double(nums):
    return tuple(num * 2 for num in nums)

테스트 케이스에서 속도의 차이는 거의 없습니다.

테스트 1 〉	통과 (0.29ms, 10.3MB)
테스트 2 〉	통과 (0.30ms, 10.4MB)
테스트 3 〉	통과 (0.29ms, 10.4MB)
테스트 4 〉	통과 (0.33ms, 10.4MB)
테스트 5 〉	통과 (0.28ms, 10.4MB)
테스트 6 〉	통과 (0.31ms, 10.4MB)
테스트 7 〉	통과 (0.35ms, 10.3MB)
테스트 8 〉	통과 (0.37ms, 10.4MB)
테스트 9 〉	통과 (0.79ms, 10.4MB)
테스트 10 〉	통과 (0.74ms, 10.4MB)
테스트 11 〉	통과 (0.80ms, 10.4MB)
테스트 12 〉	통과 (0.79ms, 10.4MB)
테스트 13 〉	통과 (0.87ms, 10.4MB)
테스트 14 〉	통과 (0.48ms, 10.3MB)
테스트 15 〉	통과 (0.55ms, 10.4MB)
테스트 16 〉	통과 (0.66ms, 10.3MB)
테스트 17 〉	통과 (0.69ms, 10.3MB)
테스트 18 〉	통과 (0.75ms, 10.4MB)
테스트 19 〉	통과 (0.90ms, 10.4MB)
테스트 20 〉	통과 (0.95ms, 10.3MB)
테스트 21 〉	통과 (0.71ms, 10.4MB)
테스트 22 〉	통과 (0.54ms, 10.3MB)
테스트 23 〉	통과 (0.77ms, 10.4MB)
테스트 24 〉	통과 (0.68ms, 10.4MB)
테스트 25 〉	통과 (0.39ms, 10.4MB)
테스트 26 〉	통과 (0.39ms, 10.4MB)
테스트 27 〉	통과 (0.69ms, 10.4MB)
테스트 28 〉	통과 (0.45ms, 10.4MB)
테스트 29 〉	통과 (0.45ms, 10.4MB)
테스트 30 〉	통과 (0.43ms, 10.3MB)

1. BFS 너비 우선 탐색을 떠올려 봅시다.

혹시 BFS에 익숙하시지 않다면, 여기를 참고합시다.

def solution(rectangle, char_x, char_y, item_x, item_y):
    limit_x, limit_y = 50, 50
    moves = ((0, 1), (0, -1), (1, 0), (-1, 0))
    arrived = set()
    que = [(char_x, char_y)]
    while que:
        now_x, now_y = que.pop(0)
        if (now_x, now_y) in arrived:
            continue
        arrived.add((now_x, now_y))
        if (now_x, now_y) == (item_x, item_y):
            print('심봤다~!')
            break
        for move_x, move_y in moves:
            next_x = now_x + move_x
            next_y = now_y + move_y
            if 1 <= next_x <= limit_x and 1 <= next_y <= limit_y:
                que.append((next_x, next_y))
    return arrived


print(solution([[1, 1, 7, 4], [3, 2, 5, 5], [4, 3, 6, 9], [2, 6, 8, 8]], 1, 3, 7, 8))

이런 점들을 방문한 뒤(원칙적으로 set은 순서를 보장하지 않습니다) 아이템을 찾을 수 있긴 합니다.
아직 정답과는 거리가 멀지만 조금씩 접근해 봅시다.

심봤다~!
{(5, 1), (3, 1), (1, 1), (8, 1), (6, 1), (5, 5), (9, 4), (3, 5), (1, 5), (8, 5), (2, 6), (6, 5), (5, 9), (3, 9), (2, 10), (6, 9), (4, 1), (2, 1), (7, 4), (5, 4), (10, 4), (4, 5), (8, 4), (2, 5), (7, 8), (5, 8), (1, 9), (4, 9), (2, 9), (1, 13), (2, 13), (11, 3), (9, 3), (3, 4), (7, 3), (1, 4), (6, 4), (4, 4), (3, 8), (7, 7), (1, 8), (6, 8), (4, 8), (3, 12), (1, 12), (5, 3), (9, 2), (3, 3), (1, 3), (10, 3), (8, 3), (2, 4), (6, 3), (5, 7), (3, 7), (1, 7), (2, 8), (6, 7), (3, 11), (2, 12), (7, 2), (5, 2), (3, 2), (10, 2), (4, 3), (8, 2), (2, 3), (7, 6), (5, 6), (4, 7), (2, 7), (1, 11), (5, 10), (4, 11), (2, 11), (9, 1), (7, 1), (1, 2), (6, 2), (4, 2), (2, 2), (9, 5), (3, 6), (7, 5), (1, 6), (8, 6), (6, 6), (4, 6), (3, 10), (1, 10), (4, 10), (1, 14)}

2. 2차원 리스트를 이용해봅시다.

일단 2차원 리스트를 만들고
거기에 각 사각형의 내부를 마킹하고
그곳은 지나가지 못하도록 해보고 싶습니다.

* 사각형의 내부, 경계, 외부를 분리해서 생각합시다.

출력하기에 50 * 50은 너무 크니까
임시로 10*10 정도로 두겠습니다.
(값을 따로 빼두면 수정할 때 편합니다.
적절히 쓰면 하드 코딩보다 가독성도 좋습니다. )

def pprint(lines):
    for line in lines:
        for num in line:
            print(f'{num:3}', end='')
        print()


def solution(rectangle, char_x, char_y, item_x, item_y):
    limit_x, limit_y = 10, 10
    moves = ((0, 1), (0, -1), (1, 0), (-1, 0))
    arrived = [[-1 for _ in range(limit_y + 1)] for _ in range(limit_x + 1)]  # 빈 곳에 -1을 채워 넣습니다.
    for x1, y1, x2, y2 in rectangle:
        for rect_x in range(x1 + 1, x2):
            for rect_y in range(y1 + 1, y2):
                arrived[rect_x][rect_y] = -2  # 각 사각형의 내부에는 -2를 둡니다.
    que = [(char_x, char_y)]
    while que:
        now_x, now_y = que.pop(0)
        if arrived[now_x][now_y] != -1:  # 재방문 방지
            continue
        arrived[now_x][now_y] = 0  # 방문한 곳은 0으로 마킹합니다.
        if (now_x, now_y) == (item_x, item_y):
            print('심봤다~!')
            break
        for move_x, move_y in moves:
            next_x = now_x + move_x
            next_y = now_y + move_y
            if 1 <= next_x <= limit_x and 1 <= next_y <= limit_y:
                que.append((next_x, next_y))
    return arrived


pprint(solution([[1, 1, 7, 4], [3, 2, 5, 5], [4, 3, 6, 9], [2, 6, 8, 8]], 1, 3, 7, 8))

흔히 보는 좌표 평면과는 좀 다르지만,
알아먹을 수는 있을 정도는 됩니다.

심봤다~!
 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
 -1  0  0  0  0  0  0  0  0  0  0
 -1  0 -2 -2  0  0  0  0  0  0  0
 -1  0 -2 -2  0  0  0 -2  0  0  0
 -1  0 -2 -2 -2  0  0 -2  0  0  0
 -1  0 -2 -2 -2 -2 -2 -2 -2  0  0
 -1  0 -2 -2  0 -1 -1 -2  0  0  0
 -1  0  0  0  0  0 -1 -2  0  0  0
 -1  0  0  0  0 -1 -1 -1 -1 -1 -1
 -1  0  0  0 -1 -1 -1 -1 -1 -1 -1
 -1  0  0 -1 -1 -1 -1 -1 -1 -1 -1

-2는 사각형의 내부, -1은 방문하지 못한 곳, 0은 방문한 곳입니다.

3. 0 대신 방문한 거리를 기록하면 어떨까?

(동적 계획법에서 이와 비슷한 접근법을 자주 쓰죠.)

def pprint(lines):
    for line in lines:
        for num in line:
            print(f'{num:3}', end='')
        print()


def solution(rectangle, char_x, char_y, item_x, item_y):
    limit_x, limit_y = 10, 10
    moves = ((0, 1), (0, -1), (1, 0), (-1, 0))
    arrived = [[-1 for _ in range(limit_y + 1)] for _ in range(limit_x + 1)]  # 빈 곳에 -1을 채워 넣습니다.
    for x1, y1, x2, y2 in rectangle:
        for rect_x in range(x1 + 1, x2):
            for rect_y in range(y1 + 1, y2):
                arrived[rect_x][rect_y] = -2  # 각 사각형의 내부에는 -2를 둡니다.
    que = [(char_x, char_y, 0)]  # 튜플에 거리 추가
    while que:
        now_x, now_y, length = que.pop(0)
        if arrived[now_x][now_y] != -1:  # 재방문 방지
            continue
        arrived[now_x][now_y] = length  # 방문한 곳에 length 기록
        if (now_x, now_y) == (item_x, item_y):
            print('심봤다~!')
            break
        for move_x, move_y in moves:
            next_x = now_x + move_x
            next_y = now_y + move_y
            if 1 <= next_x <= limit_x and 1 <= next_y <= limit_y:
                que.append((next_x, next_y, length + 1))  # 거리 +1 추가
    pprint(arrived)
    return arrived[item_x][item_y]


print(solution([[1, 1, 7, 4], [3, 2, 5, 5], [4, 3, 6, 9], [2, 6, 8, 8]], 1, 3, 7, 8))

심봤다~!
 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
 -1  2  1  0  1  2  3  4  5  6  7
 -1  3 -2 -2  2  3  4  5  6  7  8
 -1  4 -2 -2  3  4  5 -2  7  8  9
 -1  5 -2 -2 -2  5  6 -2  8  9 10
 -1  6 -2 -2 -2 -2 -2 -2 -2 10 11
 -1  7 -2 -2 12 -1 -1 -2 12 11 12
 -1  8  9 10 11 12 -1 -2 13 12 13
 -1  9 10 11 12 -1 -1 -1 -1 -1 -1
 -1 10 11 12 -1 -1 -1 -1 -1 -1 -1
 -1 11 12 -1 -1 -1 -1 -1 -1 -1 -1
13

이렇게 두고 나니 (예상했던!) 문제점이 보입니다.

최단 거리를 찾아가다 보니 건너 뜁니다.

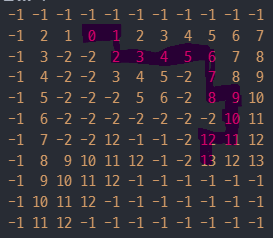
위 그림의 경로 중 (2, 3, 4, 5)를 보면 그 아래쪽의 경로는 무시되었음을 알 수 있습니다.

다시 설명하자면,
이런 부분은

-2 -2 -1 
-2 -1 -1 
-2 -1 -1 
-2 -2 -1

-1을 따라 0, 1, 2, 3, 4, 5 순서로 따라가야 하는데

이렇게 0, 1, 2, 3 으로 끝납니다.

4. 사각형의 경계만 남기면 어떨까요?

모든 사각형의 경계와 내부를 특정 숫자로 마킹한 뒤,
모든 사각형의 내부만 다른 숫자로 덮어쓰면,
전체의 경계만 남습니다.
(합집합, 교집합, 차집합의 벤다이어그램을 떠올려 보십시오.)

for문을 사용해서 쉽게 구현할 수 있고,
꽤 많은 경우의 수를 정리해 줄 것 같은 느낌적인 느낌이 딱...

반복을 줄이기 위해
모든 사각형의 경계를 특정 숫자로 마킹하고
모든 사각형의 내부를 다른 숫자로 덮었습니다.

def pprint(lines):
    for line in lines:
        for num in line:
            print(f'{num:3}', end='')
        print()


def solution(rectangle, char_x, char_y, item_x, item_y):
    limit_x, limit_y = 10, 10
    moves = ((0, 1), (0, -1), (1, 0), (-1, 0))
    arrived = [[-2 for _ in range(limit_y + 1)] for _ in range(limit_x + 1)]  # 빈 곳에 -2
    for x1, y1, x2, y2 in rectangle:  # 사각형의 테두리를 그려줍니다. 
        for rect_x in range(x1, x2 + 1):
            arrived[rect_x][y1] = -1
            arrived[rect_x][y2] = -1
        for rect_y in range(y1, y2 + 1):
            arrived[x1][rect_y] = -1
            arrived[x2][rect_y] = -1
    for x1, y1, x2, y2 in rectangle:
        for rect_x in range(x1 + 1, x2):
            for rect_y in range(y1 + 1, y2):
                arrived[rect_x][rect_y] = -2  # 각 사각형의 내부에는 -2를 둡니다.
    pprint(arrived)
    que = [(char_x, char_y, 0)]  # 튜플에 거리 추가
    while que:
        now_x, now_y, length = que.pop(0)
        if arrived[now_x][now_y] != -1:  # 재방문 방지
            continue
        arrived[now_x][now_y] = length  # 방문한 곳에 length 기록
        if (now_x, now_y) == (item_x, item_y):
            print('심봤다~!')
            break
        for move_x, move_y in moves:
            next_x = now_x + move_x
            next_y = now_y + move_y
            if 1 <= next_x <= limit_x and 1 <= next_y <= limit_y:
                que.append((next_x, next_y, length + 1))  # 거리 +1 추가
    pprint(arrived)
    return arrived[item_x][item_y]


print(solution([[1, 1, 7, 4], [3, 2, 5, 5], [4, 3, 6, 9], [2, 6, 8, 8]], 1, 3, 7, 8))

-1로 된 경계가 보입니다.

예상대로! 건너뛰기가 완벽하게 해결된 것은 아닙니다. (4, 5, 6) 참고

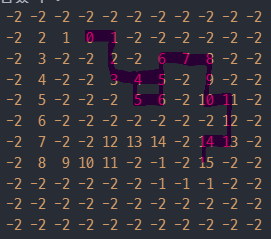
-1 이 3번 이상 반복되는 곳은 건너 뜀 현상이 없어졌지만

-2 -1 -1 -1 -2 
-2 -1 -1 -1 -2 
-2 -2 -2 -2 -2

2번 반복 되는 곳은 여전합니다.

-2 -1 -1 -2 
-2 -1 -1 -2 
-2 -2 -2 -2

5. 좌표계를 *2 해주면 해결됩니다.

"-1 이 3번 이상 반복되는 곳은 건너 뜀 현상이 없어졌지만
2번 반복 되는 곳은 여전합니다. "
라고 했습니다.

위 문장에서 아이디어를 얻어서
*2 하면 붙었던 부분이 떨어진다는 것을 떠올려보십시오.

마지막에 // 2 하는 것 잊지 마시고...

끝~!

def pprint(lines):
    for line in lines:
        for num in line:
            print(f'{num:3}', end='')
        print()


def make_double(nums):
    return tuple(num * 2 for num in nums)


def solution(rectangle, char_x, char_y, item_x, item_y):
    limit_x, limit_y = 20, 20
    rectangle = tuple(make_double(r) for r in rectangle)
    char_x, char_y, item_x, item_y = make_double((char_x, char_y, item_x, item_y))
    moves = ((0, 1), (0, -1), (1, 0), (-1, 0))
    arrived = [[-2 for _ in range(limit_y + 1)] for _ in range(limit_x + 1)]
    for x1, y1, x2, y2 in rectangle:  # 사각형의 테두리를 그려줍니다.
        for rect_x in range(x1, x2 + 1):
            arrived[rect_x][y1] = -1
            arrived[rect_x][y2] = -1
        for rect_y in range(y1, y2 + 1):
            arrived[x1][rect_y] = -1
            arrived[x2][rect_y] = -1
    for x1, y1, x2, y2 in rectangle:
        for rect_x in range(x1 + 1, x2):
            for rect_y in range(y1 + 1, y2):
                arrived[rect_x][rect_y] = -2  # 각 사각형의 내부에는 -2를 둡니다.
    que = [(char_x, char_y, 0)]  # 튜플에 거리 추가
    while que:
        now_x, now_y, length = que.pop(0)
        if arrived[now_x][now_y] != -1:  # 재방문 방지
            continue
        arrived[now_x][now_y] = length  # 방문한 곳에 length 기록
        if (now_x, now_y) == (item_x, item_y):
            print('심봤다~!')
            break
        for move_x, move_y in moves:
            next_x = now_x + move_x
            next_y = now_y + move_y
            if 1 <= next_x <= limit_x and 1 <= next_y <= limit_y:
                que.append((next_x, next_y, length + 1))  # 거리 +1 추가
    pprint(arrived)
    return arrived[item_x][item_y] // 2


print(solution([[1, 1, 7, 4], [3, 2, 5, 5], [4, 3, 6, 9], [2, 6, 8, 8]], 1, 3, 7, 8))

심봤다~!
 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2
 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2
 -2 -2  4  3  2  1  0  1  2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2
 -2 -2  5 -2 -2 -2 -2 -2  3 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2
 -2 -2  6 -2 -2 -2 -2 -2  4 -2 -2 -2 16 17 18 19 20 -2 -2 -2 -2
 -2 -2  7 -2 -2 -2 -2 -2  5 -2 -2 -2 15 -2 -2 -2 21 -2 -2 -2 -2
 -2 -2  8 -2 -2 -2 -2 -2  6  7  8 -2 14 -2 -2 -2 22 -2 -2 -2 -2
 -2 -2  9 -2 -2 -2 -2 -2 -2 -2  9 -2 13 -2 -2 -2 23 -2 -2 -2 -2
 -2 -2 10 -2 -2 -2 -2 -2 -2 -2 10 11 12 -2 -2 -2 24 25 26 -2 -2
 -2 -2 11 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 27 -2 -2
 -2 -2 12 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 28 -2 -2
 -2 -2 13 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 29 -2 -2
 -2 -2 14 -2 -2 -2 -2 -2 24 25 26 27 28 -2 -2 -2 32 31 30 -2 -2
 -2 -2 15 -2 -2 -2 -2 -2 23 -2 -2 -2 29 -2 -2 -2 33 -2 -2 -2 -2
 -2 -2 16 17 18 19 20 21 22 -2 -2 -2 30 -2 -2 -2 34 -2 -2 -2 -2
 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 31 -2 -2 -2 -1 -2 -2 -2 -2
 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 32 33 -1 -1 -1 -2 -2 -2 -2
 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2
 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2
 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2
 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2
17

ABOUT ME

ComDoc ComDoc

1. BFS 너비 우선 탐색을 떠올려 봅시다.

2. 2차원 리스트를 이용해봅시다.

3. 0 대신 방문한 거리를 기록하면 어떨까?

4. 사각형의 경계만 남기면 어떨까요?

5. 좌표계를 *2 해주면 해결됩니다.

티스토리툴바

ABOUT ME

1. BFS 너비 우선 탐색을 떠올려 봅시다.

2. 2차원 리스트를 이용해봅시다.

3. 0 대신 방문한 거리를 기록하면 어떨까?

4. 사각형의 경계만 남기면 어떨까요?

5. 좌표계를 *2 해주면 해결됩니다.

관련글 관련글 더보기

티스토리툴바