11. 비율 검정

이전까진 평균과 표준 편차를 이용해 검정을 했다.
이제 비율을 이용한 검정을 해보자.

[집에 태블릿 PC 있다] 2019년 19% → 2021년 24%

2019년 설문조사에 따르면 한국 가정의 19%가 태블릿을 가지고 있다고 한다.
2021년 무작위로 400가구를 조사했더니 96가구가 태블릿을 가지고 있었다.
(통계적 지식 없이도 전체 가구의 태블릿 보유율은 증가한 것으로 예상되지만,) 
한국 가정의 태블릿 기기를 보유율의 증감을 95% 신뢰도(양측 검정)로 검정해 보자.

 

귀무가설: 2021년 19%의 가구가 태블릿을 가지고 있다.
대립가설: 2021년 19% 이상, 또는 이하의 가구가 태블릿을 가지고 있다.

---

p = 0.19
q = 1 - 0.19 = 0.81

p위에 - 씌운 것을 p hat이라고 하는 데 ㅠ,.ㅠ
윗줄 입력이 어려우니 아쉬운 데로 아래와 같이 표현하겠다.

햇은 측정값.

pHat = 0.24
qHat = 1 - 0.24 = 0.76

---

비율 검정에는 미리 고려해야 할 점이 있다.

표본의 비율과 표본의 수를 곱한 것이 10보다 커야 한다.
pHat * n > 10
0.24 * 400 = 96 이니까 충분히 크다.

표본의 여사건의 비율과
표본의 수를 곱한 것 또한 10보다 커야 한다.
qHat * n > 10
0.76 * 400 = 304 이니까 만족한다.

모자라면 만족할 때까지
표본의 크기를 증가시키면 된다.

---

비율 검정에서 알아야 할 공식

모집단의 평균값(𝜇)은 p이며
𝜇 = p

모집단의 표준 편차(σ)는 p(1 - p)의 제곱근이다.
σ = p(1 - p) ** .5

---

이제 알아야 할 것은 모두 알았으니 분포표를 그려 놓고 생각을 하자. 

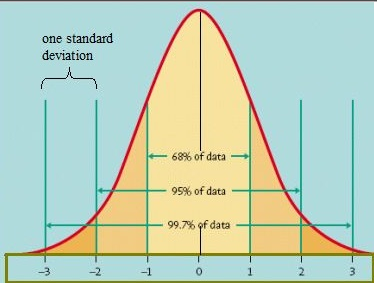
위의 공식 암기보다
아래 사고의 전환이 더 중요하다. 

중심 극한 정리를 떠올려보자.

모집단인 2019년 태블릿 보유 가구 데이터에서
400가구씩의 표본을 아주 많이 뽑은 뒤
각 표본의 태블릿 보유 비율로
분포표를 그린다면
위 분포표의 평균은 19%(=0.19) 일 것이다. 

그리고 위 공식을 이용해서 '모집단의 표준 편차'를 알 수 있다.

>>> (0.19 * (1 - 0.19)) ** 0.5
0.39230090491866065

0.39

'표본 평균의 표준 편차'를 구한다.
중심 극한 정리에 의해, 
(모집단의 표준 편차) / (표본 내의 원소수) ** 0.5

>>> ((0.19 * (1 - 0.19)) ** 0.5) / 400 ** 0.5
0.019615045245933032

0.02

---

굳이 정규화를 하지 않더라도
평균 0.19, 표준편차 0.02 라면
첫 번째 표준 편차는 0.21
두 번째 표준 편차는 0.23
세 번째 표준 편차는 0.25
임을 알 수 있다.

0.24는 두 번째와 세 번째 표준 편차 사이에 있다. 
위 그래프를 보면
2번째 표준편차는 95%
3번째 표준 편차는 99.7%
0.24은 95% 밖에 있으며
이는 문제에서 제시한 95% 의 신뢰도를 넘어선다.  

---

이것의 의미는 다음과 같다.
2021년 조사한 400가구의 데이터가 있다.
만약 이것이 2019년 조사와 차이가 없다면 (귀무가설) 

2019년 데이터에서 400개의 가구를 무한 번 뽑아서 만든 분포에서
2021년 400가구의 데이터의 위치를 찾으면, 
평균에 가까운 곳에 위치해야 한다.

그런데 이 샘플은 멀리 있다. 
드문 확률로 존재하는 표본이라는 의미이다.

그래서 우리는 이렇게 이상한 샘플이 왜 뽑혔지?

라고 반문하게 되고.

(샘플이 이상한 게 아니라면)
귀무가설이 잘못된 것이라는
결과에 도달하게 된다. 

귀무가설(2021년 19%의 가구가 태블릿을 가지고 있다)은 기각하고, 
대립가설(2021년 19% 이상 또는 이하의 가구가 태블릿을 가지고 있다)을 채택한다.

---

'드물다, 드물지 않다'는 통계에서는 '신뢰도'라고 명명되어 있다. 
신뢰도의 반대말은 유의수준.

이 문제에서는 양측 검정으로 95%라는 숫자가 주어졌고.
이것은 중심(평균)에서 95% 영역 안에 있으면
'이 샘플은 기존 샘플과 비슷하다'라고
인정하겠다는 의미이다.

유의수준은 바깥쪽부터 기준으로 5%에 있으면 많이 다르다 라고 인정하겠다는 의미.
일반적으로 양쪽 검정은 사용하고 이를 양쪽으로 나누니 2.5%

통계가 어려운 이유 중 하나가 단어가 직관적이지 않아서라고 생각한다.
단어의 의미보다는 분포 그래프 내에서의 의미에 집중하는 것이 좋을 것 같다. 

---

그럼 이제 24%에 대한 정규화를 해보자. 

0.24 - 0.19 / 0.02  

>>> (0.24 - 0.19) / (((0.19 * (1 - 0.19)) ** 0.5) / 400 ** 0.5)
2.549063709672908

2.55이다. 

표준정규분포표에서 찾아보면 0.00539 (0.539%)이다.
99% 밖에 있고 99.9% 안쪽에 있다.

 

---

참고한 기사는 다음과 같다. 
실제로는 5,100명을 조사했다고 하는데... 
이렇게 되면 표본 평균의 표준 편차가 더욱 낮아짐을 예상할 수 있고...
정규화된 숫자(z-score)는 더 커질 것이다. 
계산해 보면 9.1이 나온다. ㄷㄷㄷ 

(0.24 - 0.19) / (((0.19 * (1 - 0.19)) ** 0.5) / 5100 ** 0.5)
9.1019780212125

http://www.seouldailynews.co.kr/coding/news.aspx/6/1/16224

 

파이썬으로 사용한 코드를 정리해 보았다. 

import math


def z2p(z_score):
    return .5 * (math.erf(z_score / 2 ** .5) + 1)


def main(p, p_hat, sample_size):
    if p_hat * sample_size > 10 and (1 - p_hat) * sample_size > 10:
        p_sd = (p * (1 - p)) ** .5
        print('모집단의 표준편차:', p_sd)

        samples_mean_sd = p_sd / sample_size ** .5
        print('표본 평균의 표준편차:', p_sd)

        z_score = (p_hat - p) / samples_mean_sd
        print('z-score:', z_score)

        print(f'percent: {(1 - z2p(-z_score)) * 100:.3f}%, {z2p(-z_score) * 100:.3f}%')


main(0.19, 0.24, 400)

모집단의 표준편차: 0.39230090491866065
표본 평균의 표준편차: 0.39230090491866065
z-score: 2.549063709672908
percent: 99.460%, 0.540%