-
17. 해시(hash), 파이썬Python/파이썬 자료구조 알고리듬 2019. 6. 11. 09:17반응형
해싱은 데이터를 아주 빠르게 '삽입'하거나 '가져올 때' 사용하는 기법입니다.
하지만, 최솟값이나 최댓값을 찾을 때(전체 자료를 검색해야 할 때)는 효율이 떨어집니다.김 빠지는 이야기를 하나 하자면..
파이썬의 딕셔너리는 해시 테이블로 구현되어 있습니다..
ㅇㅇ 있는 걸 만드는 삽질을 또 해보겠습니다.주의: 직접 만든 해시 함수를 보안에 관련된 부분에 사용하는 것은 위험합니다.
해시(hash)의 개념은 각기 다른 곳에서 독립적으로 발생하였다.
1953년 1월 H. P. Luhn은 체이닝(chaining)으로 해시를 사용한 내부 IBM 비망록을 작성했다.
G. N. Amdahl, E. M. Boehme, N. Rochester, Arthur Samuel은 거의 같은 시기에 해시를 사용하는 프로그램을 제공하였다.------------------------------------------
간단한 전화번호부를 만들어 보겠습니다.
name number
--------------
Kim 7458
John 8569
Smith 1452
Michael 2563저장공간에 가나다 순으로 이름과 전화번호를 저장해볼까요?
검색은 빠릅니다. (정렬 상태에선 이진(이분) 검색을 쓸 수 있죠?)
하지만 첫 부분에 전화번호를 추가할 때
전체 전화번호를 이동해야 하는 대 참사가 일어납니다.
전화번호를 추가, 삭제할 때마다
확률적으로 절반의 전화번호를 옮겨야 합니다.그렇다면 순서대로 저장하지 않으면 되지 않을까요?
하지만 이때는 검색에 오랜 시간이 걸립니다.
하나하나 다 찾아봐야 하니까요.이런 삽질을 하지 않기 위해 해싱이 나왔습니다.
넓은 공간을 사용해, 데이터의 저장과 검색 시 시간을 줄이는 것이 해싱의 핵심입니다.'시간'과 '공간'의 trade-off(상충관계)죠.
해시를 이용해 전화번호를 저장, 검색 해봅시다.
해시 함수 작성
0. 이름을 넣으면 고유 숫자(해시 값)가 나오는 '해시 함수'를 만듭니다.
전화 번호 저장
1. 이름을 해시 함수에 넣어서 고유 숫자(해시 값)를 리턴 받습니다.
2. 해시 값을 주소로 하는 저장공간에 전화번호를 저장합니다.전화 번호 검색
1. 해시 함수에 이름을 넣고 해시 값을 리턴 받은 뒤
2. 해시 값을 주소로 하는 저장공간을 찾아 읽으면 됩니다.말은 복잡하지만아주 빠른 검색이 가능합니다.
https://en.wikipedia.org/wiki/Hash_table 간단한 해시 함수를 만들어 보겠습니다.
'이름'이라는 문자열을 '저장 공간의 주소'라는 숫자로 바꿔야 하니까,
아스키(유니)코드를 이용하면 될 것 같습니다.
각 글자의 아스키(유니)코드를 합하여 리턴하는 해시 함수를 만들어 봅시다.이 방식으론 고유 숫자(해시 값)가 겹치기 쉽겠죠?
해시 값이 겹치는 걸 충돌(collision)이라고 합니다.
우리가 만들 해시함수에서 ABC와 ACB는 충돌합니다. OTL그래도 일단 만들어 봅시다. =='
이름 해시 함수
(각 글자의 아스키코드의 합)해시 값 Kim
John
Smith
Michael75 + 105 + 109
74 + 111 + 104 + 110
83+109+105+116+104
77+105 +99 +104 +97 +101 +108289
399
517
691해시값을 주소로 바로 쓰는 것을 Direct-address table이라고 부릅니다.
하지만, 고작 4개의 전화번호를 집어넣기 위해 691개 이상의 저장공간을 만들 수는 없는 일입니다.
적당한 배열의 크기를 정하고 해시값을 배열의 크기로 나눈 나머지(% modulo 연산)를 주소로 하겠습니다.
배열의 크기는 139로 합니다.배열의 크기는 소수(prime number)를 이용하는 것이 좋다는 썰이 있지만 수학적으로 맞는 말인지는 모르겠습니다.일단 코딩해 보겠습니다.
파이썬에서 문자의 아스키(유니)코드를 얻는 함수는 ord()입니다.class Hashtable: def __init__(self): self.table_length = 139 self.table = [None for _ in range(self.table_length)] def simple_hash(self, name): ord_sum = 0 for letter in name: ord_sum += ord(letter) return ord_sum % self.table_length # return sum(map(ord, name)) % self.table_length def put(self, name, num): self.table[self.simple_hash(name)] = num def show(self): for idx, value in enumerate(self.table): if value: # is not None print(idx, value) def find(self, name): return self.table[self.simple_hash(name)]boo = Hashtable() boo.put('Kim', 7458) boo.put('John', 8569) boo.put('Smith', 1452) boo.put('Michael', 2563) print(boo.find('Kim')) # 7458여기까진 작동이 잘 됩니다만, 다음 값을 넣어보면..
boo = Hashtable() boo.put('Kim', 7458) boo.put('John', 8569) boo.put('Smith', 1452) boo.put('Michael', 2563) boo.put('Raymond', 1598) boo.put('Clayton', 7532) boo.show()11 7458 35 7532 100 1452 121 8569 135 2563Raymond의 전화번호 '1598'이 사라졌습니다.
이것은 앞서 ABC, BCA로 설명드렸듯 Raymond와 Clayton은 같은 해시값을 가지기 때문입니다.
이를 해결하려면 (해시값이 겹치지 않도록) 해시 함수가 더 넓은 범위의 숫자를 생성할 수 있도록 수정해야 합니다.
'호너의 룰(다항식을 표현하는 방법)'을 응용해서 넓혀 보겠습니다.
반복적으로 숫자를 곱한 뒤 더하면 됩니다.
아래 예에서는 소수인 37을 사용했습니다.말은 복잡하지만 소스를 보면 단순합니다.def put(self, name, num): self.table[self.better_hash(name)] = num def find(self, name): return self.table[self.better_hash(name)] def better_hash(self, name): honer = 37 ord_sum = 0 for letter in name: ord_sum = ord_sum * honer + ord(letter) return ord_sum % self.table_length # from functools import reduce # return reduce(lambda acc, cur: acc * 37 + cur, map(ord, name)) % self.table_lengthboo = Hashtable() boo.put('Kim', 7458) boo.put('John', 8569) boo.put('Smith', 1452) boo.put('Michael', 2563) boo.put('Raymond', 1598) boo.put('Clayton', 7532) print(boo.find('Kim')) print(boo.find('John')) print(boo.find('Smith')) print(boo.find('Michael')) print(boo.find('Raymond')) print(boo.find('Clayton')) # boo.show()7458 8569 1452 2563 1598 7532정상적으로 출력이 되었습니다.
하지만, 아무리 해시 함수를 잘 짜도 충돌을 완벽하게 피할 수는 없습니다.
그래서 충돌 처리가 필요합니다.충돌 처리
위 예제에서는
간략하게 코딩하기 위해서
전화번호만 저장했습니다.하지만 충돌이 발생했을 때
누구의 번호인 지 알 수 있으려면
이름과 전화번호를 같이 저장해야 합니다.충돌처리는 코드 없이 개념만 이야기하겠습니다.
분리된 체인(Separate chaining)
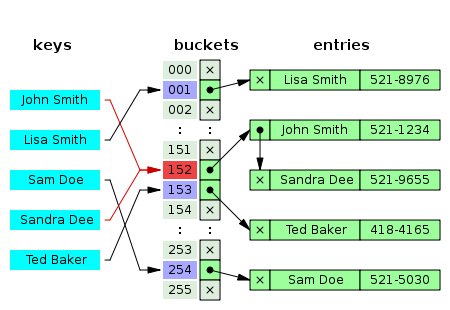
https://en.wikipedia.org/wiki/Hash_table 연결 리스트를 이용합니다.
체인이 길어지면 검색이 느려질 수 있습니다.
추가적인 메모리가 필요한 단점이 있습니다.오픈(개방) 주소 해싱
보통 해시 테이블에는 빈 공간이 많습니다.
추가적인 공간을 만들지 않고 기존에 해시 테이블 공간만으로 충돌을 해결하는 것입니다.
주소를 다른 데이터에게 개방한다는 뜻이겠죠?오픈 주소 해싱은 선형 조사(탐사), 제곱 조사, 이중 해싱 등이 있습니다.
선형 조사(Linear Probing)
충돌이 발생하면 해시 테이블의 다음 요소가 비어있는지 확인합니다.
비어 있으면 저장...추가적인 메모리가 필요하지 않은 장점이 있습니다.
단점은 한번 충돌이 발생하면 그 주위에 충돌이 몰리는 군집화 현상이 발생하기 쉽습니다.또 삭제가 조금 복잡합니다.
충돌이 발생했을 때의 마지막 요소는 삭제하면 됩니다.
하지만 마지막이 아닌 요소들은 그냥 삭제할 수 없습니다.
빈 공간이 되어 버리면 검색이 끊어지니까요.
이럴 때는 삭제 후 연결 더미(dummy)를 넣어서 해결합니다.제곱 조사(Quadratic probing)
선형 조사는 고정폭으로 다음 요소가 비어있는지 확인합니다.
제곱 조사는 폭을 제곱으로 늘리면서 다음 요소가 비어있는지 확인합니다.
군집화를 막기 위한 방법입니다.이중 해싱(double hashing)
이중 해싱은 해싱 함수를 2개 만들어 충돌 시 2번째 함수를 이용하는 겁니다.
2번째 함수가 조사 시 이동 폭을 결정합니다.
제곱 조사보다 좀 더 발전(?)한 방법입니다.파이썬 해시 관련 기능
그런데
사실 이 고생을 할 필요가 없었던(?) 것이파이썬에는 hash() 함수가 있습니다. --;파이썬에는 배터리 포함(battery include)이라는 개념이 있습니다.
박 대리배터리가 포함된 물건을 구입하면 바로 사용할 수 있듯..
웬만한 건 다 포함해 놓겠다는 뜻입니다.하지만 ㅠ,.ㅠ 프로그램을 재시작할 때마다 해시 값이 달라집니다.
파이썬 3.3부터 달라졌다고 합니다. OTL 해킹 예방의 이유로..더보기해시값이 고정되어 있으면,
이를 예측할 수 있게 되고,
해킹이 가능해 지기 때문에,
salted(원 데이터에 어떤 숫자나 문자 등을 더한 뒤 해시를 해,
해시값의 변화를 주는) 방식으로 바뀌었다고 합니다.옛 코드들과의 호환을 위해
PYTHONHASHSEED 환경변수를 0으로 세팅하면 고정된다고 하는데,
굳이 해킹 방지를 위해 막아둔 기능을 다시 살릴 이유는 없어 보입니다.프로그램을 재시작할 때마다 해시값이 달라지기 때문에,
프로그램 시작할 때마다 해시값이 달라져도 문제없을 때,
즉 일시적으로 메모리에 데이터를 저장할 때는 사용할 수 있을 것 같습니다.(그럴 땐 딕셔너리를 쓰라고~!)하지만, 데이터를 디스크에 저장할 때 저 해시값을 이용하다간...
재시작할 때마다 해시값이 달라져서 데이터를 못 찾게 되겠죠?(그럴 땐 딕셔너리를 피클로 저장하면 되잖아~!)내장 함수(BIF)로 해시를 출력해 보았습니다.
print(hash('Kim')) print(hash('John')) print(hash('Smith')) print(hash('Michael')) print(hash('Raymond')) print(hash('Clayton'))1020180751873777590 4283442748951831694 -3739260113697835183 2029863934088486807 -8584650091868107534 -9017698407008398061재실행하니 값이 달라지네요.
-1150927097311894257 7757377576672179676 3936194327126680892 7539443892000353034 3666183309139244587 -8768861275962404916암호학적 해시 함수
파이썬의 기본 라이브러리 중에는 hashlib도 있습니다.
암호화와 관련된 해싱 라이브러리입니다.import hashlib h = hashlib.sha256() h.update(b'Kim') result = h.hexdigest() print(result)d25949ef9e762fe7cfb9cc5d125e8a7bbca56662abc51b9d0dc0d2265aa28dce해시를 쓰다 보니
해시의 특징 및 장점이 발견되고,
이를 암호화에 응용, 발전하게 됩니다.대표적인 것이 '패스워드 저장'과 '파일의 체크섬 확인'입니다.
암호화폐에도 쓰고.패스워드 저장
해시 함수는 해시값에서 역으로 원본을 찾기가 아주 어렵습니다.
이것을 '단방향성'이라고 하는데요.
서버에서 사용자의 암호를 저장할 때 응용합니다.단방향성을 쉽게 설명하자면
위 예시 코드(엉터리!해시함수)의 mod(%) 연산을 보시면 됩니다.'% 139'의 결과가 해시값이기 때문에
해시값은 0~138까지의 숫자가 되며,
해시값만으론 원래 이름은 알 수가 없습니다.'ABC'와 'BCA', 'CAB'가 같은 해시값을 가진다면,
이 들 중 뭐가 원래 이름인지 알 수 없죠.위의 예에서 42로 Kim을 만들 수는 없지 않습니까?
그런데 패스워드를 저장하기 위한 용도라면
'% 139'는 큰 문제가 됩니다.
어떤 패스워드를 넣던지
0~138중에 하나의 해시값을 가지게 되니까
(=충돌, collision)
몇 번만 시도를 하면 훅 뚫려버리는
아주 취약한 암호체계가 되는 거죠.자주충돌이 발생한다.
충돌 저항성이 부족하다.단방향성과 충돌저항성을 동시에 가져야 좋은 해시함수입니다.
서버에서 암호를 해싱하지 않고 '그대로 저장'했다가
서버의 사용자의 아이디와 암호가 유출되면,
해당 서버만 뚫리는 것이 아니라.
사용자가 같은 아이디, 암호를 사용하는
다른 사이트까지 뚫려버리게 됩니다.만약 패스워드 그대로가 아닌
패스워드의 '해시값만을 저장'해 두었다면,
패스워드(정확히는 해시값)들이 유출되어도,
원 패스워드를 찾기가 어렵습니다.
그래서 해킹당한 사이트뿐만 아니라,
다른 사이트까지 해킹이 퍼지는 걸 막을 수 있습니다.패스워드의 해시값만 저장했을 경우
관리자도 원 패스워드를 복원할 수 없습니다.예전에 패스워드를 분실하면
이-메일로 패스워드를 보내주던 사이트들은
이런 개념 없이 만들어진 것입니다.
아주 보안에 취약한 사이트입니다.잘 설계된 해시 함수를 사용했다면,
탈취한 해시값으로
원 패스워드를 찾는 방법은 한 가지뿐입니다.A부터 ZZZZZ... 까지를
(숫자나 특수기호를 포함하면 더 복잡해집니다)
하나하나 입력해서 해시값을 뽑은 뒤,
탈취한 해시값들과 비교하는 수밖에 없습니다.시간이 엄청 걸리는 일입니다.
그래서 해커(크래커)들은 미리 예상 패스워드-해시값 사전을 만들어 둡니다. --;사전에 있는 단어를 패스워드로 쓰면 일사천리로 패스워드가 유출됩니다.
이러한 사전을 이용한 공격을 dictionary 공격이라고 합니다.패스워드-해시값 사전의 용량은 어마 무시하기 때문에
이걸 줄인 것을 rainbow table이라고 합니다만...
자세히 알 필요는 없는 부분이죠.해시 함수를 잘 만드는 건 어려운 일입니다.
검색을 조금만 해보면 '박살난’ SHA-1, 퇴출 가속화되나?' 등의 기사를 볼 수 있습니다.
'SHAttered SHA-1'에서 'shattered'(박살난)라는 표현이 재미있습니다.전문가가 설계한 해시 함수도 이런데...
만약 비 전문가가 만든다면...그래서 해시 함수는 만드는 게 아니라고 합니다.
목적에 맞고 안전한 함수를 잘 골라 써야죠.전 세계의 보안 전문가의 검증을 통과한
보안성 높은 해시함수는 몇 개 되지 않습니다.더보기정부나 기관에서는 해시함수에 백도어를 심기도 합니다.
그리고 안전하다고 홍보하죠.
http://weekly.tta.or.kr/weekly/files/20194626054634_weekly.pdf그런데 함수의 종류가 한정되어 있다면,
사전 공격에 취약하지 않겠습니까?그래서 서버에서 패스워드를 저장할 때 '솔트(salt)'를 씁니다.
만약 'abc'라는 패스워드에 '8#K@5)'를 추가해서 해시함수에 입력하면,
'abc'의 해시값과는 전혀 다른 해시값이 나옵니다. (눈사태 효과)
이때 '8#K@5)'를 솔트라고 합니다.
음식에 소금을 치듯 패스워드에 솔트를 칩니다.
salt를 꼭 추가합시다.키 스트레칭(key stretching)이라는 방법도 있습니다.
해시값을 또 해시 함수에 넣어 반복합니다.
해시에 걸리는 시간을 늘리는 효과가 있습니다."전화번호를 기록하기 위한 해싱과,
비밀번호를 저장하기 위한 해싱과,
체크섬을 위한 해싱은
조금씩 차이가 있습니다."체크섬 확인
체크섬 확인은 파일의 확인에 사용합니다.
제가 인터넷에 파일을 하나 공개한다고 합시다.
파일이 커서 블로그에는 올리기 힘든 상황입니다.
파일은 다른 서비스를 통해 공개하고,
블로그에는 '해시함수'와 (원본 파일을 해시함수에 넣어서 나온) '해시값'만 올려둡니다.악의를 가진 누군가가 파일을 조작해서 인터넷에 유포한다고 해도...
제 블로그에 올라와 있는 해시 함수를 이용해 해시값을 비교해 보면...
조작된 파일은 전혀 다른 해시값을 가지기 때문에.. (눈사태 효과)
원본 유무를 알 수 있습니다.그런데~!!! 위에서도 살짝 언급된 부분이지만~!!!
SHA-1의 경우 조작된 PDF로 똑같은 해시값이 나오도록 한 케이스가 있습니다.이런 조작을 하는 데 사용된 연산량이 약 9경(9,223,372,036,854,775,808) 회,
단일 CPU 연산으로는 6천500년, 단일 GPU 연산으로는 110년분이라고 합니다.
즉 2017년 기준 GPU 110개를 쓰면 1년 정도 걸린다는 뜻인데요.일반인이 구할 수 있는 메인보드에도
8개의 GPU를 달 수 있는 시대입니다. (채굴용)
2020년의 GPU 성능은 또 2017년보다 향상되었으니...
채굴용 컴퓨터 10대 정도를 돌린다면...
1년 안에 해킹이 가능...
시간과 비용의 압박이 있긴 하겠지만...
일반인도 시도해 볼 수 있는 해킹인 거죠..딕셔너리
파이썬의 딕셔너리도 해시라고 했습니다.
그런데 파이썬 3.6 이후 버전에서는 딕셔너리도 순서가 유지됩니다.
아래처럼 저장 구조를 바꾸었기 때문입니다.좀 더 자세히 알고 싶으시다면...
출처 : https://blog.sinwoobang.me/post/176050610602/pythondictorderFor example, the dictionary: d = {'timmy': 'red', 'barry': 'green', 'guido': 'blue'} is currently stored as: entries = [['--', '--', '--'], [-8522787127447073495, 'barry', 'green'], ['--', '--', '--'], ['--', '--', '--'], ['--', '--', '--'], [-9092791511155847987, 'timmy', 'red'], ['--', '--', '--'], [-6480567542315338377, 'guido', 'blue']] Instead, the data should be organized as follows: indices = [None, 1, None, None, None, 0, None, 2] entries = [[-9092791511155847987, 'timmy', 'red'], [-8522787127447073495, 'barry', 'green'], [-6480567542315338377, 'guido', 'blue']]반응형